اشتباهات، مغالطه ها و سفسطه های ریاضی

اشتباهات دیگری هستند که یک شهود نادرست، مسبب آن‌هاست، از قبیل قاعده اشتباه مشتق‌گیری مانند 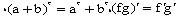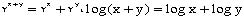و نظایر این‌ها یا حالا اشتباه دیگری که در آن ممکن است دانش‌آموز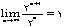  در نظر بگیرید. در واقع این اشتباه، شاید از شهودی می‌آید که در آن 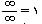 که البته در مواردی هم درست است یا اشتباهات دیگری که دانش‌آموز از قاعده‌هایی استفاده می‌کند که در حالت‌هایی درست هستند، اما در حالت به‌کار گرفته شده درست نیستند، مثل دانش‌آموزی که می‌پندارد ضرب دو عدد مثبت صرف‌نظر از اینکه صحیح یا کسری باشند، همواره از خود آن دو عدد بزرگتر یا مساوی است. نگارنده به یاد می‌آورد سر یک کلاس وقتی نشان داده شد که اعداد گنگ در تناظر یک‌به‌یک با اعداد گویا نیستند، دانش‌آموزی اعتراض کرد که مگر اعداد گویا و گنگ یک در میان نیستند؟! شاید برای این دانش‌آموز، این شهودِ اشتباه، استنتاجی از این احکام باشد که بین هر دو عدد گویای متمایز یک عدد گنگ وجود دارد و بین هر دو عدد گنگِ متمایز یک عدد گویا وجود دارد.

بعضی اوقات، حتی نام‌گذاری مفاهیم و اشیای ریاضی، می‌تواند دانش‌آموزان را به اشتباه بیندازد. مثلاً گاهی دانش‌آموزان اصطلاح «بسته» را که مفهومی در آنالیز و توپولو‌ژی است، با مفهوم «کرانداری» اشتباه می‌گیرند. شاید یک علت چنین اشتباهی این باشد که از نظر زبانی، «بسته» به‌طور ناخودآگاه محصور بودن در یک مرز محدود را در ذهن القاء کند. حتی ممکن است دانش‌آموز، «بسته» و «باز» را به‌خاطر معنی لغوی آن‌ها نقیض همدیگر بگیرد.

اشتباهات دیگری هم هستند که جنبه منطقی دارند. یک نمونه بارز در این زمینه موقعی است که از شاگرد خواسته می‌شود نشان دهد حکم خاصی با حذف یکی از مفروضاتش برقرار نیست. بسیاری از اوقات مشاهده شده است که شاگرد به جای ارائه مثال نقض، بیان می‌کند که چون استدلال حکم، بدون فرضِ حذف شده کار نمی‌کند، پس این شرط حذف شده لازم است.

همچنین در بعضی مواقع، شاگردان از یک راه نادرست به یک پاسخ درست می‌رسند، که البته در چنین شرایطی متقاعد کردن آن‌ها همیشه کار زیاد ساده‌ای نیست!

سفسطه یا پارادوکس

بین سفسطه و پارادوکس تفاوت است، زیرا پارادوکس ریاضی تناقضی است که معمولاً با یک استدلال موجه حاصل می‌شود. پارادوکس موجب ایرادهایی جدی به اصول، تعریف‌ها یا مفروضات شده و گاهی مجبور می‌شویم در آن‌ها تجدید نظر کنیم، یا آن‌ها را به‌طور دقیق‌تری بیان کنیم. از این منظر، پارادوکس‌ها باعث می‌شوند نسبت به استوار کردن شالوده‌های ریاضیات، اهتمام بورزیم. اما سفسطه تناقضی است که از یک استدلال با ظاهر صحیح، اما در باطن تقلبی، به دست آمده است. البته سنخ سفسطه در ریاضیات با گونه‌های نظیر آن در فلسفه یا علوم دیگر، متفاوت است. قبحی که گاهی برای سفسطه و سوفسطائیان در بعضی از علوم وجود دارد، شاید در ریاضیات چندان وجود نداشته باشد. یک دلیل این است که در ریاضیات، تشخیص درستی برهان، کمتر محل مناقشه است و سفسطه و سوفسطائیان خطری جدی در این علم تلقی نمی‌شوند. در لغت‌نامه انگلیسی آکسفورد، سوفسطائی² را این طور توصیف کرده است: فردی که یک استدلال هوشمندانه اما مغالطه‌آمیز به‌کار می‌بندد.

سفسطه‌های ریاضی اشتباه‌هایی هستند که فریبنده‌تر و چیره‌دستانه‌تر هستند و وجه نهفته حقیقت در آن‌ها، نسبتاً قابل توجه است. این خطاها و اشتباهات می‌توانند از منظر ریاضی، گاهی بسیار جالب و آموزنده باشند. معلمان باتجربه واقفند که تا چه حد توضیح یک اشتباه غیربدیهی برای کلاس، می‌تواند از نظر آموزشی ارزشمند باشد. حتی این موضوع در زندگی هم پیش می‌آید که بشر از اشتباهات و شکست‌هایش، بیشترین درس را می‌آموزد. اشتباهات جالب، معمولاً از علم و دانش نشأت می‌گیرند و حتی بعضی از آن‌ها در حالت‌هایی، می‌توانند نشانه نبوغ تلقی شوند. بدین سبب در بعضی مواقع، اشتباهات در ریاضیات به خاطر بُعد آموزشی آن‌ها، تا حدودی تحسین شده‌اند. لمب³ استاد دانشگاه یوتا در «وبلاگی درباره وبلاگ‌های ریاضی⁴» روی سایت انجمن ریاضی آمریکا، هم قافیه با نقل قول مشهوری از تولستوی می‌نویسد «راه‌حل‌های درست همه شبیه هستند، اما راه‌حل‌های نادرست هر کدام به شیوه خود نادرست هستند.»

در بخش بعد، چند نمونه از این سفسطه‌ها یا مغالطه‌ها که بیشتر ماهیت هندسی دارند، بیان می‌شوند. همه مواردی که می‌آیند، سفسطه‌های شناخته شده و قدیمی‌اند، اما به قولی «روح نو بین در تنِ حرف کهن». برای برانگیختن بیشتر حس کنجکاوی، از بیان جایی که اثباتش سفسطه‌آمیز است، اجتناب کرده‌ایم.

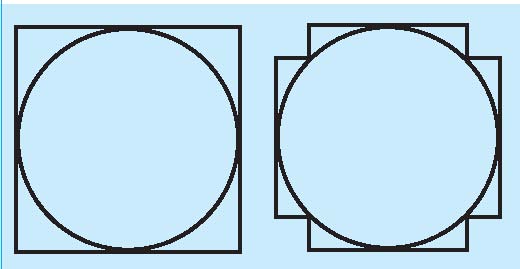
مغالطه 4= π

یک دایره به قطر 1 در نظر بگیرید. محیط این دایره برابر با π است.

این دایره را در یک مربع به ضلع 1 محاط می‌کنیم. محیط این مربع برابر با 4 است. حال به صورت زیگزاگی، گوشه‌های این مربع را ببرید و آن را به دو گوشه کوچک‌تر تقسیم کنید.

شکل 16 گوش به دست می‌آید. با ادامه این فرایند در هر مرحله، چندضلعی‌ای حاصل می‌شود که محیط آن همچنان 4 است و به دایره میل می‌کند. پس 4=π!

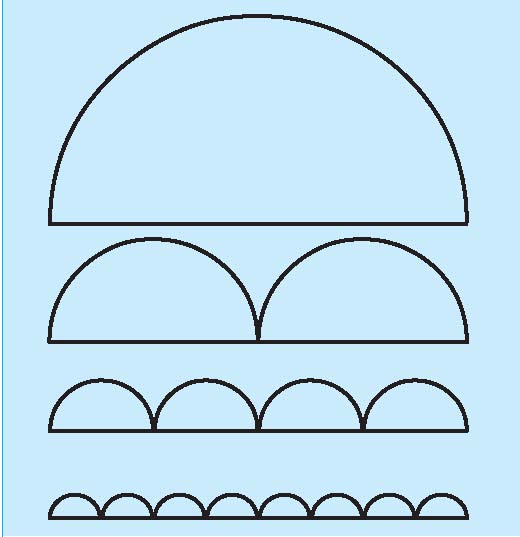
مغالطه 2= π

یک پاره‌خط به طول 1 در نظر می‌گیریم و روی آن، n نیم‌دایره هر کدام به قطر 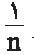 رسم می‌کنیم.

محیط هر کدام از این نیم دایره‌ها برابر با  است. بنابراین مجموع محیط شکل حاصل، برابر با 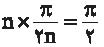 می‌شود. وقتی n زیاد می‌شود، این نیم‌دایره‌ها به پاره‌خط نزدیک می‌شوند و طول آن‌ها به طول پاره‌خط نزدیک می‌شود، پس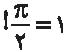

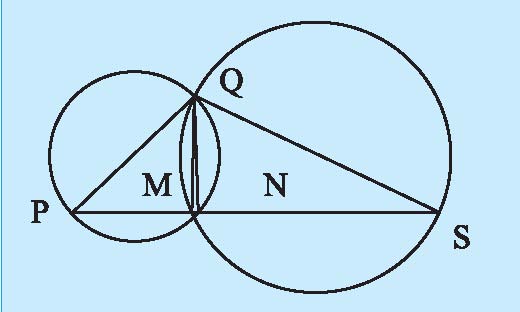
مغالطه رسم دو عمود از یک نقطه بر یک خط

یک نقطه Q خارج از یک پاره‌خط PS در نظر می‌گیریم. دایره‌هایی به قطر QP و QS رسم می‌کنیم. پاره‌خط PS، این دو دایره را در نقاط M و N قطع می‌کند. زاویه QMS با توجه به اینکه روبه‌روی قطر QS است، قائمه است. به همین ترتیب زاویه QNP با توجه به اینکه روبه‌روی قطر PQ است قائمه است. پس QM و QN دو عمود از Q بر خط واصل بین P و S هستند!

مغالطه هم‌ نهشتی دو مثلث به حالت ض‌ض‌ز

فرض کنید برای دو مثلث ABC و ʹCʹBʹA داشته باشیم، ʹA'B=AB و ʹB'C=BC و 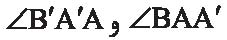 یعنی  به حالت ض‌ض‌ز هم‌نهشت هستند. با توجه به اینکه دو زاویه 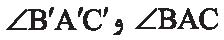با هم برابرند، نتیجه می‌شود دو زاویه 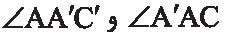نیز با هم برابرند. پس مثلث AAC' متساوی‌الساقین است، یعنی C'ʹAC=A ، در نتیجه دو مثلث ABC وʹCʹBʹA به حالت ض‌ض‌ض با هم، هم‌نهشت هستند!

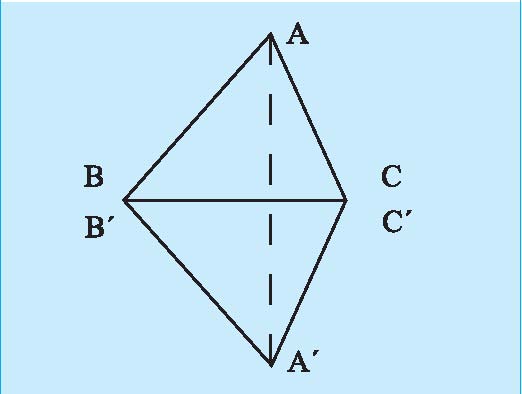
مغالطه متساوی‌ الساقین بودن هر مثلث

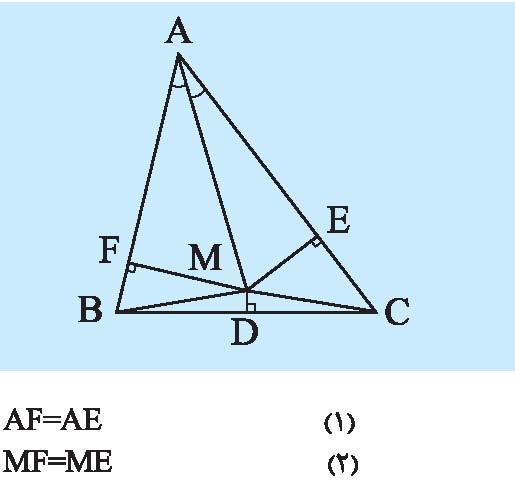
مثلث دلخواه ABC را در نظر بگیرید. فرض کنید D نقطه وسط BC باشد. محل تقاطع نیمساز زاویه A و عمودمنصف ضلع BC را M می‌نامیم. کنید F پای عمودِ فرود آمده از M بر ضلع AB و E پای عمودِ فرود آمده از M بر ضلع AC باشد. مثلث قائم‌الزاویه AMF و AME به حالت وتر و یک زاویه با هم هم‌نهشت هستند. پس خواهیم داشت.

از سوی دیگر، چون MD عمود منصف ضلع BC است، پس MB=MC. از تساوی اخیر و رابطه‌ (2) نتیجه می‌شود که دو مثلث قائم‌الزاویه MFB و MEC به حالت وتر و یک ضلع، با هم هم‌نهشت هستند. در نتیجه خواهیم داشت.

(3)                              FB=EC

از دو رابطه (1) و (3) نتیجه می‌شود AB=AC پس مثلث  ABCمتساوی‌الساقین است!

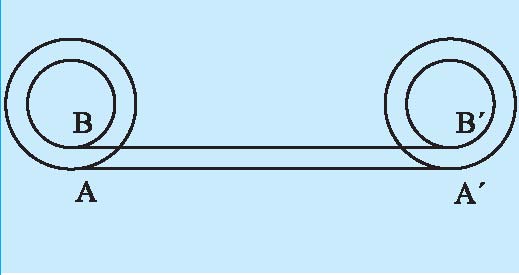
مغالطه برابر بودن محیط هر دو دایره

دو دایره هم‌مرکز را در نظر می‌گیریم. تصور کنید که این دو دایره به صورت یک چرخ درآمده باشند. این چرخ را روی یک خط مستقیم آن قدر می‌غلطانیم تا نقطه تماسِ اولیه A با خط، دوباره روی همان خط قرار گیرد، نقطه جدید A را Aʹ می‌نامیم. در این فرایند، A به اندازه محیط دایره بزرگتر را طی می‌کند تا به Aʹ برسد. پس طول AAʹ برابر با محیط دایره بزرگ‌تر است. با همین استدلال، طول BBʹ برابر با محیط دایره کوچک‌تر است. چون AAʹ و BBʹ با هم برابرند، نتیجه می‌شود محیط دو دایره با هم برابرند!

مغالطه در اثبات محاسبه مجموع زوایای داخلی یک مثلث

فرض کنید مجموع زوایای داخلی مثلث برابر با α باشد. پس در مثلث ABD داریم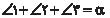

به‌طور مشابه در مثلث ADC به دست می‌آوریم.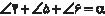

با جمع کردن دو رابطه اخیر به‌دست می‌آید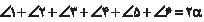

اما چون دو زاویه  مکمل هستند پس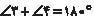

بنابراین به‌دست می‌آید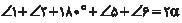

اما 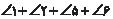مجموع زوایای داخلی مثلث ABC است که برابر با α است. پس به دست می‌آید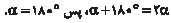

منابعی برای مطالعه بیشتر

کتاب‌های زیادی درباره اشتباه‌ها، مغالطه‌ها، پارادوکس‌ها و سفسطه‌های ریاضی نوشته‌اند. یکی از این کتاب‌ها، منبع [3] نوشته نورتروپ است که در سال 1350 تحت عنوان «معماهای ریاضی، حیله‌های جبری و هندسی، مغالطات و تناقضات» توسط محمد رکنی قاجار (از زبان فرانسوی) ترجمه شده و به وسیله انتشارات یکان چاپ شده که ظاهراً در حال حاضر، این کتاب خارج از چاپ است. یک کتاب دیگر در این زمینه منبع [2] نوشته ماکسول است که تحت عنوان «مغالطه‌های ریاضی» توسط غلامرضا یاسی‌پور ترجمه شده و انتشارات محراب قلم در سال 1380 آن را چاپ کرده است. یک کتاب قدیمی‌تر و منبع [1] هم توسط لیتسمان و تریر با عنوان «اشتباه کجاست؟» نوشته شده است (چاپ اول، سال 1913) که یکی از سرچشمه‌های اصلی کتاب‌های معرفی شده محسوب می‌شود. در این منبع، بسیاری از اشتباه‌های ریاضی مورد بررسی قرار می‌گیرند. در شماره‌های پیشین مجله رشد آموزش ریاضی، مقاله‌های متعددی به بررسی اشتباه‌های ریاضی پرداخته‌اند که از جمله، می‌توان به مقاله با عنوان «منشأ خطاهای دانش‌آموزان» نوشته بن‌زیو اشاره کرد که خلاصه‌ای از این منبع، توسط سپیده چمن‌آرا در مجله رشد آموزش ریاضی (دوره 29، شماره 2، زمستان 1390) ترجمه و چاپ شده است و در آن، نویسنده به بررسی خطاهای معقول ریاضی پرداخته است. در مقاله «پارادوکس‌های هندسی» نیز (مجله رشد برهان متوسطه 2، دوره 21، شماره 74، تابستان 1393) فرزاد حمزه‌پور به بررسی سه سفسطه هندسی پرداخته است. یکی سفسطه متساوی‌الساقین بودن هر مثلث و دیگری، رسم دو عمود از یک نقطه بر یک خط داده شده است که در این مقاله هم بررسی شدند. همچنین یک سفسطه دیگر نیز در مورد منفرجه بودن زاویه قائمه در مقاله «مغالطه‌های ریاضی» (مجله رشد برهان دوره متوسطه 2، دوره 25، شماره 94، اردیبهشت 1395) توسط احسان یارمحمدی نوشته شده است که در آن، به دو مغالطه هندسی، یکی متساوی‌الساقین بودن هر مثلث (با روش مثلثاتی) و دیگری مغالطه قرار داشتن هر نقطه درون یک دایره روی محیط آن، بررسی شده است.

پی‌ نوشت‌

1. منظور از شاگرد، هم دانش‌ آموز و هم دانشجوست و معادل student است.

2. Sophist

3. Evelyn Lamb

4. Blog on Math Blogs, (http://blogs.ams.org/blogonmathblogs/)

منابع

[1] Lietzmann, W. and Trier, O. (1913). “Wo steckt der Fehler? Trugschlüsse und Schülerfehler.” Leipzig: B. G. Teubner. IV+57 S. kl. 8° (Math. Bibl. X) (1913).

[2] Maxwell, E. A. (1959). Fallacies in mathematics Cambridge University Press, New York.

[3] Northrop, E. P. (1959). “Riddles in mathematics. A book of paradoxes.” London: The English Universities Press Ltd. X, 242 p. (1959).